问题
问答题
设2，2，1是3阶矩阵A的特征值，对应的特征向量依次为
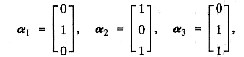求矩阵A及An．
答案
参考答案：按特征值特征向量的定义有 Aα1=2α1， Aα2=2α2， Aα3=α3．用分块矩阵表示，得到 A(α1，α2，α3)=(2α1，2α2，α3)．
因为α1，α2，α3线性无关，矩阵(α1，α2，α3)可逆，故
A=(2α1)，2α2，α3)(α1，α2，α3)-1
[*]
由于矩阵A有3个线性无关的特征向量，矩阵A可以相似对角化，有
[*]
[*]
解析：[*]