问题
单项选择题
已知x1、x2是方程x2-(3k+1)x+(3k2-2k+3)=0的两个实根,则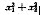 的最小值是()。
的最小值是()。
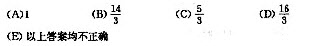
A.A
B.B
C.C
D.D
E.E
答案
参考答案:E
解析:
由韦达定理,x1+x2=3k+1,x1x2=3k2-2k+3,故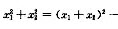 2x1x2=3k2+10k-5,而又△=(-(3k+1))2-4(3k2-2k+3)≥0,即1≤k≤
2x1x2=3k2+10k-5,而又△=(-(3k+1))2-4(3k2-2k+3)≥0,即1≤k≤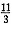 .由抛物线图线的性质可以得知,当k=1时
.由抛物线图线的性质可以得知,当k=1时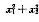 的最小值为8.
的最小值为8.
已知x1、x2是方程x2-(3k+1)x+(3k2-2k+3)=0的两个实根,则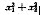 的最小值是()。
的最小值是()。
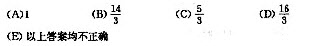
A.A
B.B
C.C
D.D
E.E
参考答案:E
解析:
由韦达定理,x1+x2=3k+1,x1x2=3k2-2k+3,故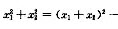 2x1x2=3k2+10k-5,而又△=(-(3k+1))2-4(3k2-2k+3)≥0,即1≤k≤
2x1x2=3k2+10k-5,而又△=(-(3k+1))2-4(3k2-2k+3)≥0,即1≤k≤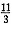 .由抛物线图线的性质可以得知,当k=1时
.由抛物线图线的性质可以得知,当k=1时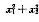 的最小值为8.
的最小值为8.