问题
单项选择题
若方程（k2+1）x2-（3k+1）x+2=0有两个不同的正根，则k应满足的条件是（）。
A.k＞1或k＜-7
B.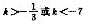
C.k＞1
D.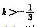
E.以上答案均不正确
答案
参考答案：C
解析：
设方程的两根分别为x1，x2，则有x1＞0，x2＞0且x1≠x2．由韦达定理得，x1+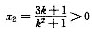
，即要求3k+1＞0，得
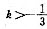．又根据△=(3k+1)2-8(k2+1)=k2+6k-7=(k-1)(k+7)＞0，知k＞1或k＜-7，综合上述各限制条件可以得出k的最终限制范围，即k＞1．