问题
问答题
一渔船停泊在距海岸9公里处，今需派人送信给距渔船
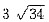公里处的海岸渔站．如果送信人步行每小时5公里，船速每小时4公里，问应在何处登岸再走，才可使抵达渔站的时问最短
答案
参考答案：如图2—2—2所示，设渔船A到海岸BC的距离AB=9，A与渔站C的距离[*]
则[*]
[*]
假设在离渔站x公里处登陆，那么自A到C所需时间为
[*]
于是[*]
令 t’=0，
则有 25(15-x)2=16[92+(15-x)2]，
即 (15-x)2=144，
解得 x=3∈(0，15)．
当z∈(0，3)，有t’＜0，当x∈(3，15)，有t’＞0，故当x=3时，t有极小值，即最小值(因在区间(0，15)内只有一个驻点，而最小值存在)，也就是当登陆点离渔站3公里处，所用的时间最省．
解析：
[分析]： 这是导数应用的题．由题设，先列出所需时间的表达式，再按求极值的方法，算出所用时间的最小值．