问题
问答题
设f(x)在[a，b]上存在一阶导数，且|f’(x)|≤M，
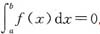．证明：当x∈[a，b]时，
．
答案
参考答案：命[*]，有φ(a)=φ(b)=0，故在(a，b)内|φ(x)|存在最大值点x=x0．若|φ(x0)|=0，则|φ(x)|=O，结论自然成立．若|φ(x0)|≠0，则φ(x0)总是φ(x)的极值(极大值或极小值)．于是φ’(x0)=0．由泰勒公式，
[*]
以φ(a)=0，φ(b)=0分别代入上式，并且注意到φ’(x0)=0，φ’(x)=f(x)，于是有
[*]
[*]
于是
[*]
无论是[*]，还是[*]，总可得[*]，于是有[*]