问题
问答题
设
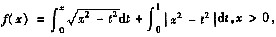
(Ⅰ)求f(x)在(0,+∞)的最小值点;
(Ⅱ)f(x)在(0,+∞)是否存在最大值并说明理由.
答案
参考答案:[分析与求解] (Ⅰ)由定积分的几何意义知
[*]
(这是以原点为心,半径为x的圆在第一象限部分的面积).
再用分段积分法求f(x)表达式中的另一积分:
当0<x<1时
[*]
当x≥1时
[*]
于是[*]
为求f(x)在(0,+∞)上的最小值,先求f’(x).
[*]
由[*]
[*]
f(x)在(0,+∞)的最小值点是[*]
(Ⅱ)由于[*]故
[*]
所以f(x)在(0,+∞)不存在最大值.
