问题
问答题
求幂级数
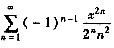 的收敛域及和函数.
的收敛域及和函数.
答案
参考答案:[分析与求解] 求[*]
及其收敛域,令[*]转化为求
[*]
及其收敛域.由于
[*]
因为逐项求导数保持幂级数的收敛半径不变[*]②与③有相同的收敛半径R=1,回到原问题[*]①有收敛半径[*]且.
[*]
于是[*]
在收敛区间端点[*]幂级数[*]是收敛的,又[*]处连续,因此
[*]
解析:[评注] ①利用逐项求志或逐项积分的方法求幂级数的收敛域与和函数时,往往可以不必先求收敛半径,而是利用逐项求导或逐项积分保持收敛不变的性质,由已知逐项求导或逐项积分后幂级数的收敛半径而求得原幂级数的收敛半径,然后再验证收敛区间端点的敛散性而求得收敛域。
②这是缺项幂级数(有无穷多项系数数为零),若先求它的收敛半径时,不能直接用求R公式,只能用如下两种方法:
[*]
