问题
问答题
证明不等式
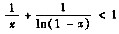当x＜1且x≠0时成立．
答案
参考答案：[分析与证明] 由[*]可得
[*]
又因当x＜0时ln(1-x)＞0，而当0＜x＜1时ln(1-x)＜0，故当x＜1且x≠0时总有xln(1-x)＜0，于是
[*]
考察函数f(x)=x+ln(1-x)-xln(1-x)，知f(0)=0，且
[*]
故f(x)当x≤0时单调减少，从而f(x)＞f(0)=0当x＜0时成立，又f(x)当0≤x＜1时单调增加，从而f(x)＞f(0)=0当0＜x＜1时成立．综合即得f(x)＞0当x＜1且x≠0时成立．这表明不等式[*]当x＜1且x≠0时成立．