假设某公司有这样一个运用新技术的开拓型项目，其目前需要投资5000万元，无建设期，项目预计使用寿命为4年，各年预期产生的税后现金净流量见下表。
单位：万元
假设项目包含有风险因素的贴现率为20% (其中无风险报酬率为8%)。如果通过该项目的实施，证明新技术是成功的，则该公司将新技术运用于商业化项目生产，其规模将是开拓型项目的3倍。即在第四年末，该公司可以进行新一轮的投资，其投资规模是开拓型项目的3倍，即1.5亿元，其每年预期可产生的经营税后现金净流量均为开拓型项目相应年份现金净流量的3倍(见下表)。
要求：
(1)分别通过计算评价不考虑期权条件下的开拓型项目和商业化项目的可行性；
(2)如果考虑期权因素，界定商业化项日的期权属性；
(3)由于该项目所运用的技术不确定性程度较高，可比公司股票价格的标准差为35%，可以作为该项目现金流量的标准差，利用布莱克—斯科尔斯期权定价模型，计算商业化项目的的价值；
(4)如果考虑期权因素，评价开拓型项目的可行性。
参考答案：
(1)不考虑期权条件下的开拓型项目和商业化项目的净现值：
开拓型项目的净现值=-5000+1000×(P/S，20%，1)+2000×(P/S，20%，2)+ 3000×(P/S，20%，3)+1000×(P/S，20%，4)
=-5000+1000×0.8333+2000×0.6944+3000×0.5787+1000×0.4823
=-5000+833.3+1388.8+1736.1+482.3
=-559.5(万元)
商业化项目的净现值=-15000×(P/S，8%，4)+[3000×(P/S，20%，1)+6000×(P/S，20%，2)+9000×(P/S，20%，3)+3000×(P/S，20%，4)]×(P/S，20%，4)
=-15000×0.735+(3000×0.8333+6000×0.6944+9000×0.5787+3000×0.4823)×0.4823
=-11025+4440.5×0.4823
=-11025+2141.65
=-8883.35(万元)
由于开拓型项目和商业化项目的净现值均小于零，所以，不考虑期权条件下的开拓型项目和商业化项目均不可行。
(2)如果考虑期权因素，商业化项目属于扩张期权，即该期权是以商业化项目为标的资产、执行价格为商业化项目的投资额、到期日为4年的欧式看涨期权。
(3)利用布莱克一斯科尔斯期权定价模型，计算该期权的的价值：
商业化项目的投资额15000万元是期权的执行价格，执行价格的现值(按无风险折现率折现为11025万元[=15000/(1+8%)4]；商业化项目经营现金流量的现值为4440.5万元(相当于第四年年底的数额)，折现到第一年年年初为2141.65万元[=4440.5/(1+20%)4]，为期权标的资产的目前价格。
根据布莱克—斯科尔斯期权定价模型计算：
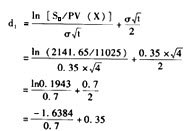
=-2.3406+0.3536
=-1.987
d2=d1-σ×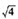
=-1.987-0.35×2
=-1.987-0.7
=-2.687
通过N(1.98)=0.9761和N(1.99)=0.9767之间插值来计算N(1.987)：
N(1.987)=0.9761+×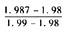
(0.9767-0.9761)=0.9765
N(-1.987)=1-N(1.987)=1-0.9765=0.0235
通过N(2.68)=0.9963和N(2.69)=0.9964之间插值来计算N(2.687)：
N(2.687)=0.9963+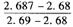
×(0.9964-0.9963)=0.9964
N(-2.687)=1-N(2.687)=1-0.9964=0.0036
C0=S0N(d1)-PV(X)N(d2)
=2141.65×0.0235-11025×0.0036
=50.33-39.69
=10.64(万元)
该期权的的价值为10.64万元，它也是该商业化项目的价值。
(4)如果考虑期权因素，上述开拓型项目的价值是-559.5+10.64=-548.86万元，因此该开拓型项目是不可行性。
注意：本题是按教材的思路来做的，严格来讲这种做法不符合布莱克一斯科尔斯期权定价模型的要求，原因是期权执行价格的现值11025万元[=15000/(1+8%)4]不是按连续复利计算的，按布莱克一斯科尔斯期权定价模型的要求，期权执行价格的现值应按连续复利计算，应为10892.46万元[=15000×e-8%×4]。