参考答案：由特征方程

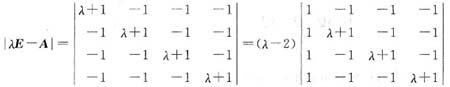
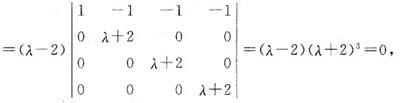
知λ=2，λ=-2(三重根)．
λ=2时，(2E-A)X=0，即

，(每行元素之和为0)
得

(只有一个线性无关特征向量)．
λ=-2时，(-2E-A)X=0，即

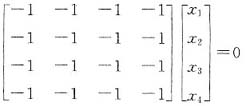
同解方程为x₁+x₂+x₃+x₄=0，
对应特征向量为(取正交特征向量)
ξ₂=[1，-1，0，0]^T，ξ₃=[1，1，-2，0]^T，ξ₄=[1，1，1，-3]^T．
当有解ξ₂后，求ξ₃时，ξ₃与ξ₂正交，且又满足方程，当有解ξ₂，ξ₃，求ξ₄时，令ξ₄和ξ₂，ξ₃正交，且满足方程．