下述命题
①设f(x)在任意的闭区间[a,b]上连续,则f(x)在(-∞,+∞))上连续.
②设f(x)在任意的闭区间[a,b]上有界,则f(x)在(-∞,+∞)上有界.
③设f(x)在(-∞,+∞)上为正值的连续函数,则
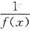 在(-∞,+∞)上也是正值的连续函数.
在(-∞,+∞)上也是正值的连续函数.
④设f(x)在(-∞,+∞)上为正值的有界函数,则
 在(-∞,+∞)上也是正值的有界函数.
在(-∞,+∞)上也是正值的有界函数.
其中正确的个数为( ).
参考答案:B
解析:
[分析]: ①与③是正确的,③与④是不正确的,正确的个数为2.
①是正确的.理由如下:设x0∈(-∞,+∞),则它必含于某区间[a,b]中.由于题设f(x)在任意闭区间[a,b]上连续.故在x0处连续,所以在(-∞,+∞)上连续.证论的关键之处是:函数f(x)的连续性是接点来讨论的.在区间上每一点连续.就说它在该区间上连续.
②函数f(x)在[a,b]上有界性的“界”是与区间有关的.例如f(x)=x在区间[a,b]上,|f(x)|≤max{|a|,|b|}[*]M.这个“界”,与区间[a,b]有关.容易看出,在区间(-∞,+∞)上,此f(x)=x就无界了.②不正确.
③是正确的.其理由是:设x0∈(-∞.+∞),所以f(x0)>0且f(x)在x0处连续,由连续函数的四则运算知,[*]在x0处也连续,所以[*]≥在(-∞,+∞)上连续.
④是不正确的.例如函数[*],在区间(-∞,+∞)上0<f(x)≤1,所以f(x)在(-∞,+∞)上有界,而[*]在(-∞,+∞)上无界.这是因为当x→±∞时[*].
