问题
问答题
设
，问a，b，c为何值时，向量组α1，α2，α3与β1，β2，β3是等价向量组，向量组等价时求α1由β1，β2，β3线性表出的表出式及β1由α1，α2，α3线性表出的表出式．
答案
参考答案：将[α1，α2，α3
β1，β2，β3]一起作初等行变换，有
[A|B]=[α1，α2，α3
β1，β2，β3]=
=[α’1，α’2，α’3|β’1，β’2，β’3]=[A’|B’]．
向量组
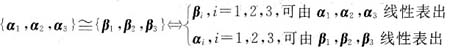
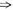r(A)=r(B)．故应取a=1，b=2，c=-2．
当a=1，b=2，C=-2时，
[A’|B’]=[α’1，α’2，α’3
β’1，β’2，β’3]
，故{α’1，α’2，α’3}≌{β’1，β’2，β’3}，从而有{α1，α2，α3)≌{β1，β2，β3}．求β1由α1，α2，α3线性表出的表出式，即解方程组
得通解为k[-1，-1，1]T+[1，0，0]T，即β1=(-k+1)α1-kα2+kα3，其中k是任意常数．求α1由β1，β2，β3线性表出的表出式，即解方程
得通解为l[-4，1，2]T+[1，0，O]丁，即α1=(-4l+1)β1+lβ2+2lβ3，其中l是任意常数．