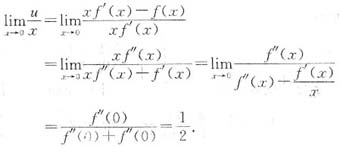问题
问答题
设f(x)具有二阶连续导数,f(0)=0,f’(0)=0,f’(0)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作切线,此切线在z轴上的截距记为u,求
 .
.
答案
参考答案:由于f’(0)=0及f"(0)>0,故当x≠0时,f’(x)≠0.过点(x,f(x))(x≠0)的切线方程为Y-f(x)=f’(x)(X-x).令Y=0得截距
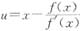 .从而
.从而
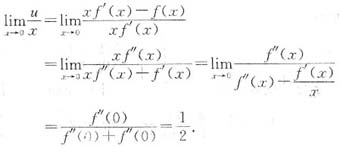
设f(x)具有二阶连续导数,f(0)=0,f’(0)=0,f’(0)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作切线,此切线在z轴上的截距记为u,求
 .
.
参考答案:由于f’(0)=0及f"(0)>0,故当x≠0时,f’(x)≠0.过点(x,f(x))(x≠0)的切线方程为Y-f(x)=f’(x)(X-x).令Y=0得截距
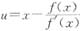 .从而
.从而