参考答案：若f(x)有三个或三个以上零点，则由罗尔定理知，f’(x)至少有两个零点．对f’(x)再用罗尔定理知，f"(x)至少有一个零点．与题设f"(x)无零点矛盾．以下证f(x)至少有一个零点．
设f’(0)=a＞0，由泰勒公式：

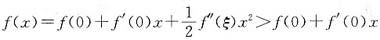，当x≠0，取

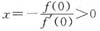，有f(x)＞0．由介值定理知，在区间(0，+∞)上f(x)至少有一个零点．又因当x＞0时f’(x)＞f’(0)＞0，故在区间(0，+∞)上至多有一个零点，故正好有一个零点．
设f’(0)=a＜0，类似可证在区间(-∞，0)上正好有一个零点．
设f’(0)=a=0，由连续函数保号性及f’(x)严格单增知，存在δ＞0，当x∈[0，δ]时f(x)＜0且f’(δ)＞0．
在点x=δ处用泰勒公式，有

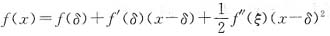
＞f(δ)+f’(δ)(x-δ)， 当x＞δ．
取

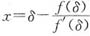，有f(x)＞0．由介值定理知，在区间(δ，+∞)上f(x)至少有一个零点．又因当x＞0时，f’(x)＞f’(0)=0．故在区间(0，+∞)上至多有一个零点．故正好有一个零点．同理可证，此时在区间(-∞，0)上也正好有一个零点．
故总之，不论f’(0)=a＞0，＜0，=0，f(x)在(-∞，+∞)上至少有一个零点．
证毕．