问题
问答题
设函数f(x)在[0,π]上连续,在(0,π)内可导,且
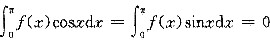 .试证:存在ξ∈(0,π),使f’(ξ)=0.
.试证:存在ξ∈(0,π),使f’(ξ)=0.
答案
参考答案:因sinx>0,x∈(0,π),又由题设
[*]
若在(0,π)内f(x)恒正,则[*].
若在(0,π)内f(x)恒负,则[*].
故在(0,π)内f(x)不可能恒正或恒负,因而f(x)在(0,π)内必有零点.
下面证明f(x)在(0,π)内零点不唯一.
设α∈(0,π)是f(x)的唯一零点,则对于x≠α,x∈(0,π),有sin(x-α)f(x)必恒正或恒负(否则f(x)必另有零点),即有,但由题设知
[*]
此与[*]矛盾.这就说明f(x)在(0,π)内零点的个数不止一个.于是由罗尔定理知,在f(x)的两个零点之间必存在ξ∈(0,π),使f’(ξ)=0.
解析:
[分析]: 欲证ξ∈(0,π),使f’(ξ)=0,关键是要证明在(0,π)内f(x)有两个以上的零点,于是由罗尔定理知,存在ξ∈(0,π),使f’(ξ)=0.
