施工网络图中,若结点0和6分别表示起点和终点,则关键路径为()
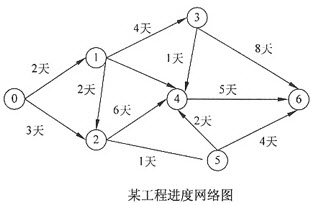
A.0→1→3→6
B.0→1→4→6
C.0→1→2→4→6
D.0→2→5→6
参考答案:C
解析:
关键路径法(Critical Path Method,CPM)是借助网络图和各活动所需时间(估计值),计算每一活动的最早或最迟开始和结束时间。CPM法的关键是计算总时差,这样可决定哪一个活动有最小时间弹性。
CPM算法的核心思想是将WBS分解的活动按逻辑关系加以整合,统筹计算出整个项目的工期和关键路径。
在网络图中(AOE)的某些活动可以并行地进行,所以完成工程的最少时间是从开始顶点到结束顶点的最长路径长度,称从开始顶点到结束顶点的最长路径为关键路径(临界路径),关键路径上的活动为关键活动。
为了找出给定的AOE网络的关键活动,从而找出关键路径,先定义几个重要的量:
Ve(j)、Vl(j):顶点j事件最早、最迟发生时间。
e(i)、l(i):活动i最早、最迟开始时间。
从源点Vl到某顶点Vj的最长路径长度,称为事件Vj的最早发生时间,记做Ve(j)。Ve(j)也是以Vj为起点的出边<Vj,Vk>所表示的活动ai的最早开始时间e(i)。
在不推迟整个工程完成的前提下,一个事件Vj允许的最迟发生时间,记做Vl(j)。显然,l(i)=Vl(j)-(ai所需时间),其中j为ai活动的终点。满足条件l(i)=e(i)的活动为关键活动。
求顶点Vj的Ve(j)和Vl(j)可按以下两步来做:
(1)由源点开始向汇点递推
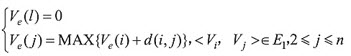
其中,E1是网络中以Vj为终点的入边集合。
(2)由汇点开始向源点递推
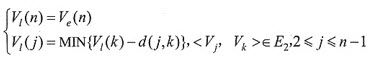
其中,E2是网络中以Vj为起点的出边集合。
由此,我们可以求出关键路径是0→1→2→4→6,正确答案是C。
