问题
填空题
设(x0,y0)是抛物线y=ax2+bx+c上的一点,若在该点的切线过原点,则系数应满足的关系是______.
答案
参考答案:
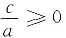 或
或
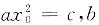
解析:[考点提示] 先求出过点(x0,y0)的切线方程,再将原点坐标代入切线方程即可.
[解题分析] y’=2ax+b,y’(x0)=2ax0+b,
过(x0,y0)点的切线方程为
y-y0=(2ax0+b)(x-x0),即[*]此切线过原点,把x=y=0代入上式,得
[*]
所以系数应满足的关系式为[*]或[*]任意.
