问题
问答题
设二维随机变量(X，Y)的概率密度为
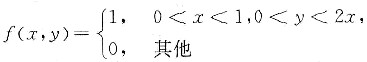
求：(Ⅰ)(X，Y)的边缘概率密度fX(x)，fY(y)；
(Ⅱ) Z=2X-Y的概率密度fz(z)；
(Ⅲ)
答案
参考答案：根据题意可得
(Ⅱ) 记FZ(Z)为z的分布函数，
D={(x，y)|0＜x＜1，0＜y＜2x}，
D1={(x，y)|0＜x＜1，Y＞0，2x-y＞z＞0}，
根据题意可知(X，Y)服从D上的均匀分布．D1是D的子区域，于是
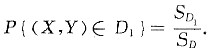
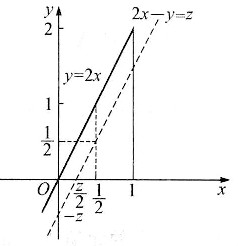
由右图可知，
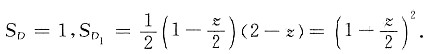
当0＜z＜2时，有
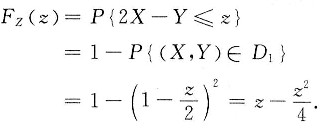
当z≤0时，有FZ(z)=0；当z≥2时，有FZ(z)=1．所以z的概率密度为
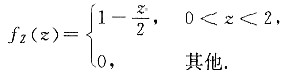
(Ⅲ) 如图，记
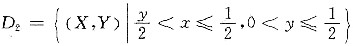，则D2是一个直角梯形，且
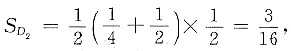
于是
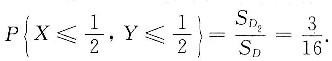
记
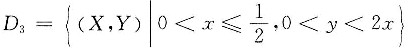，有
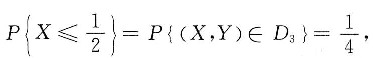
所以
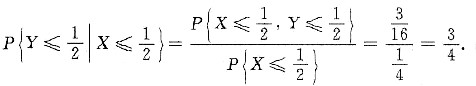
解析：[考点提示] 二维随机变量的概率密度．