问题
选择题
已知奇函数f(x)在定义域[-2,2]内递减且满足f(1-m)+f(1-m2)<0,则实数m的取值范围为( )
A.(-1,1)
B.[-1,1]
C.[-1,1)
D.(-1,1]
答案
依题设f(1-m)+f(1-m2)<0 f(1-m)<-f(1-m2)
又因 f(x)奇函数
故-f(1-m2)=f(m2-1)
f (1-m)<f(m2-1)
因为函数在定义域[-2,2]内递减
故1-m>m2-1,即m2+m-2<0
即-2<m<1
又因函数f(x)的定义域是[-2,2],
故-2≤1-m≤2且-2≤1-m2≤2,
即-1≤m≤3且-
≤m≤3 3
最后综合得-1≤m<1
故选C

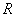 ,
,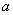 卫星离地面的高度等于
卫星离地面的高度等于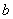 卫星离地面高度为
卫星离地面高度为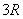 ,则:
,则:
 是多少?
是多少?