参考答案：B

解析：

要按照题目要求填结点，那么，左下角的结点n7应当具有最小值，也就是1，右下角的结点n6，应当具有最大值，也就是9。如图8-19所示，现在考虑将2、3、4、 5、6、7、8放入其中。

现在，不考虑n7和n6，在要放入数值的树中，其左下角结点为n4，放入剩余数字的最小值2，根据题目对此树的要求，n8应当放入3。右下角结点为n3，放入剩余数字的最大值为8，根据题目要求，n1应当放入7。结果如图8-20所示。

现在只剩下4、5、6了，根据题目要求，显然应当在n2放入4，n5放入5，n6放入6。最终结果如图8-21所示。所以，第1空的正确答案为选项G，第2空的正确答案为选项D，第3空的正确答案为选项F。

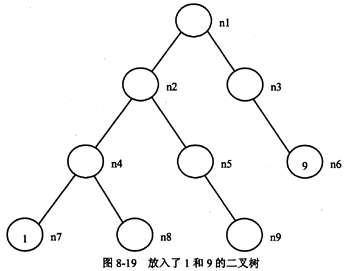
要使此树保持题目要求的特点，放入3.5，那么，可放到n8下面，作为它的右子树。第4空的正确答案为选项B。