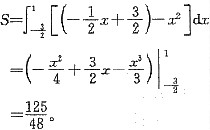问题
问答题
设抛物线y=x2与该曲线在点(1,1)处的法线所围平面图形为D,求D的面积。
答案
参考答案:
先求法线。
由f’(x)=2x可知f’(1)=2。
所以y=x2在(1,1)处的法线斜率为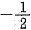 ,因此法线方程为
,因此法线方程为
化简得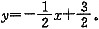
作出平面图形D,如图阴影部分所示。

下面先求法线 与曲线y=x2的交点的横坐标,因为
与曲线y=x2的交点的横坐标,因为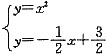
所以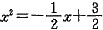 ,因此2x2+x-3=0,从而
,因此2x2+x-3=0,从而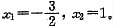
平面图形D的面积S为
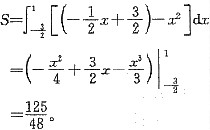
设抛物线y=x2与该曲线在点(1,1)处的法线所围平面图形为D,求D的面积。
参考答案:
先求法线。
由f’(x)=2x可知f’(1)=2。
所以y=x2在(1,1)处的法线斜率为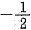 ,因此法线方程为
,因此法线方程为
化简得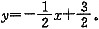
作出平面图形D,如图阴影部分所示。

下面先求法线 与曲线y=x2的交点的横坐标,因为
与曲线y=x2的交点的横坐标,因为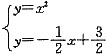
所以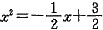 ,因此2x2+x-3=0,从而
,因此2x2+x-3=0,从而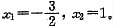
平面图形D的面积S为