顶点A的轨迹方程是x²-=1(x＞1).

如图所示,

以直线BC为x轴，线段BC的中垂线为y轴建立直角坐标系.

∵|BC|=4，∴B（-2，0），C（2，0），

由2sinC=2sinB+sinA，利用正弦定理可得

2|AB|=2|AC|+|BC|，

即|AB|-|AC|=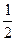|BC|=2＜4，

即点A到点B的距离与到点C的距离之差是常数2.

由双曲线的定义可知，点A的轨迹是以B、C为焦点的双曲线的右支（除顶点）.

其中，2a=2,∴a=1.2c=4.∴c=2.从而b²=c²-a²=3.

∴顶点A的轨迹方程是x²-=1(x＞1).