问题
问答题
设
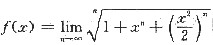 (x>0).
(x>0).
求:(1)求f(x)的表达式;
(2)讨论f(x)的连续性.
答案
参考答案:[详解] (1)1°因为根式中有xn和[*]项,使用夹逼定理时必须知道xn和[*]的大小.
由[*],得[*]
即 当0<x<2时,[*],
当x≥2时,[*]
2°由1°知,讨论极限时必须分段如下:(0,1],(1,2),[2,+∞)
(i)当0<x≤1时,[*]
[*]
[*]
(ii)当1<x<2时(注意:[*]),
此时xn>1,[*],
[*]
即[*]
[*]
(iii)当x≥2时(注意:[*])
此时[*]
[*]
(2)因为f(1+0)=f(1-0)=f(1),∴f(x)在x=1连续.
f(2+0)=f(2-0)=f(2),∴f(x)在x=2连续.
∴f(x)是(0,+∞)上的连续函数.
解析:
[分析]: n→∞时的极限与x的不同取值有关.
[评注] 确定f(x)的定义域分成(0,1],(1,2),[2,+∞)是关键.
