问题
问答题
设f(x)与g(x)在(a，b)内可导，且f’(x)+f(x)g’(x)≠0，试证明：
(1)在(a，b)内方程f(x)=0至多有一个实根；
(2)如果f(x)为连续函数，且恒有
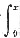f(t)dt＞f(x)，试证明：对任意x≠0，积分
．
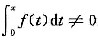答案
参考答案：[详解] (1)用反证法
设f(x)=0在(a，b)中至少有两个实根，
例如f(x1)=f(x2)=0，
其中：a＜x1＜x2＜b．
令ψ(x)=f(x)eg(x)，则ψ(x1)=ψ(x2)=0．
则由罗尔定理：[*]∈(a，b)使F’(ξ)=0．
则f’(ξ)+f(ξ)g’(ξ)=0与题设矛盾，所以在(a，b)内f(x)=0至多有一个实根．
(2)今[*]，则F’(x)=f(x)．
由条件知F(x)＞F’(x)，取g(x)=-x，则g’(x)=-1，
所以F(x)＞F’(x)相当于F’(x)+F(x)g’(x)＜0．
由(1)知F(x)在(-∞，+∞)至多有一个实根．
因为F(0)=0，所以[*]
解析：
[分析]： 使用反证法，并构造辅助函数ψ(x)=f(x)eg(x)．
[评注] 由若干小题构成一个大题，经常做后面小题时要用到前面小题的结论．