问题
问答题
设二次型f(x1，x2，x3)=
-2x1x2-2x1x3+2αx2x3，通过正交变换化为标准形
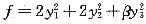，求常数α，β及所用正交变换矩阵Q，若XTX=3，求f的最大值．
答案
参考答案：[详解] 二次型及其对标准形的矩阵分别为
[*]A的特征值为2，2，β．
|A-λE|=0，则[*]
于是α2+2α+1=0，解得α=-1．
又A～B，于是2+2+β=a11+a22+a33=3，则β=-1．
可知A的特征值为2，2，-1．
(i)A的属于λ=2的特征向量：
[*]
x1=-x2-x3，[*]
单位化，得[*](ξ1，ξ2已经正交)．
(ii)A的属于λ=-1的特征向量：
[*]
单位化，得[*]
所用正交变换矩阵Q=(η1，η2，η3)=[*]
由通过变换x=Qy可化为[*]这里xTx=yTQTQy=yTy=3．
于是 [*]
故f在xTx=3下的最大值是6．
解析：
[分析]： 通过正交变换化二次型为标准形，说明前后二次型所对应矩阵是相似的，由此可求出参数α、β的取值，再按通常方法求正交矩阵Q即可．化为标准形后，条件XTX=3可等价表示为YTY=3．再将标准形适当放大，即可利用条件YTY=[*]求得最大值．
[评注] ①若A、B相似，则最常用的两个结论是：[*]，由此可确定有关参数；
②本题ξ1，ξ2已经正交，否则应先将ξ1，ξ2正交化·再单位化．
