问题
填空题
已知ξ1,ξ2,ξ3是线性非齐次方程组Ax=b的三个线性无关解向量,β1=a1ξ1+a2ξ2+a3ξ3,β2=b1ξ1+b2ξ2+b3ξ3,β3=c1ξ1+c2ξ2+c3ξ3,是对应线性齐次方程组Ax=0的解,则
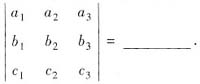
答案
参考答案:0
解析:
[分析]: 因Aξi=b,i=1,2,3.故
A(a1ξ1+a2ξ2+a3ξ3) =a1Aξ1+a2Aξ2+a3Aξ3=(a1+a2+a3)b.
但a1ξ1+a2ξ2+a3ξ3是Ax=0的解,则有(a1+a2+a3)b=0,由于b≠0,从而得
a1+a2+a3=0.
同理有 b1+b2+b3=0,
c1+c2+c3=0.
于是
[*]
