问题
问答题
作变换t=tanx,把方程
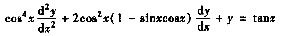
变换成y关于t的微分方程,并求原方程的通解.
答案
参考答案:[分析与求解] (Ⅰ)先求[*]
将它们代入原方程得
[*]
即[*]
(Ⅱ)求解这个常系数线性方程:
相应的特征方程λ2+2λ+1=0,有重特征根λ=-1.
非齐次方程的特解y*=t-2.
因此方程(*)的通解为 y=(C1+C2t)e-t+t-2.
(Ⅲ)原方程的通解为 y=(C1+C2tanx)e-tanx+tanx-2.
