问题
问答题
假设总体X的概率密度为
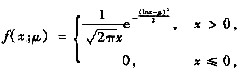
其中μ为未知参数，且X1，X2，…，Xn是来自总体X的一个简单随机样本．
(Ⅰ)求参数μ的最大似然估计量
;
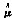(Ⅱ)验证
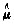是的无偏估计量．
答案
参考答案：记样本的似然函数为L(μ)，对于总体X的样本值x1，x2，…，xn，其似然函数
[*]
当xi＞0时(i=1，2，…，n)，对L(μ)取对数并对μ求导数，得
[*]
令(1nL)’=0，得驻点[*]不难验证[*]就是L(μ)的最大值点，因此μ的最大似然估计量为
[*]
(Ⅱ)首先求lnX的分布．
[*]
由于被积函数f(s)恰是正态分布N(μ，1)的密度，因此随机变量1nX服从正态分布N(μ，1)，即ElnX=μ，[*]的无偏估计量．
[*]