问题
问答题
设函数f(x)在[0,+∞)上连续,且f(x)>0,令
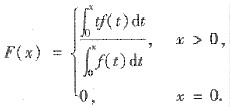
试证:F(x)在[0,+∞)上单调增加.
答案
参考答案:因为f(x)>0,连续,所以当x>0时,F(x)=[*]连续,可导.
又[*]
即F(x)在x=0处右连续,所以F(x)在[0,+∞)上连续.
又当x>0时,
[*]
记[*],则
[*]
因此当x>0时,ψ(x)单调增加,即有g(x)>g(0)=0,故当x>0时,F’(x)>0.
所以F(x)在[0,+∞)上单调增加.
解析:[考点] 证明函数在所给区间上严格单调增加
