资料:
C公司在2001年1月1日发行5年期债券,面值1000元,票面年利率10%,于每年12月31日付息到期时一次还本。
要求:
(1) 假定2001年1月1日金融市场上与该债券同类风险投资的利率是9%,该债券的发行价应当定为多少
(2) 假定1年后该债券的市场价格为1049.06元,该债券于 2002年1月1日的到期收益率是多少
(3) 该债券发行4年后该公司被揭露出会计账目有欺诈嫌疑,这一不利消息使得该债券价格在2005年1月1日由开盘的 1018.52元跌至收盘的900元。跌价后该债券的到期收益率是多少(假定能够全部按时收回本息)
(4) 假设证券评级机构对它此时的风险估计如下:如期完全偿还本息的概率是50%,完全不能偿还本息的概率是50%。当时金融市场的无风险收益率8%,风险报酬斜率为0.15,债券评级机构对违约风险的估计是可靠的,请问此时该债券的价值是多少
参考答案:
(1) 发行价=100×(P/A,9%,5)+1000×(P,9%, 5)
=100×3.8897+1000×0.6499
=388.97+649.90
=1038.87元
(2) 用9%和8%试误法求解:
V(9%)=100×(P/A,9%,4)+1000×(P,9%,4)
=100×3.2397+1000×0.7084
=1032.37元
V(8%)=100×(P/A,8%,4)+1000×(P,8%,4)
=100×3.3121+1000×0.7350
=1066.21元
插补法求解:
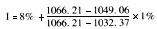
=8%+(17.15/33.84)×1%
=8.5%(或8.51%)
(3) 900=1100/(1+i)
1+i=1100/900=1.2222
跌价后到期收益率=22.22%
(4) 现金流入期望值=550
标准差
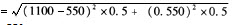
=550
变化系数=550/550=1
要求的收益率K=无风险收益率+风险附加
=无风险收益率+风险报酬率×变化系数
=8%+0.15×1=23%
债券价值V=550/(1+23%)=447.15元
