问题
填空题
设
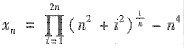 ,则
,则
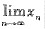 =______.
=______.
答案
参考答案:25e-4+2anctan2
解析:[考点] 求数列极限(与定积分定义相关联)
[答案解析] 对xn取对数后,化为和式极限:
[*]
经变形得
[*]
右端为对f(x)=ln(1+x2)对[0,2]进行2n等分后,取[*][*](i=1,2,…,2n)后的一个积分和,于是由f(x)在[0,2]连续,必可积得
[*]
设
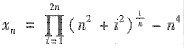 ,则
,则
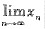 =______.
=______.
参考答案:25e-4+2anctan2
解析:[考点] 求数列极限(与定积分定义相关联)
[答案解析] 对xn取对数后,化为和式极限:
[*]
经变形得
[*]
右端为对f(x)=ln(1+x2)对[0,2]进行2n等分后,取[*][*](i=1,2,…,2n)后的一个积分和,于是由f(x)在[0,2]连续,必可积得
[*]