函数
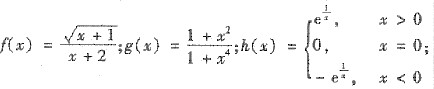ψ(x)≠0连续，且存在常数k＞0，使
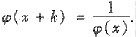分别讨论这四个函数在其定义域内的有界性．
参考答案：(1)f(x)的定义域Df=[-1，+∞)，取a=[*]，b=1．用公式：[*]，得[*]+2)，故[*]，即f(x)在定义域上有界．
(2)对任意实数x∈Dg=(-∞，+∞)，由[*]+x4)．得[*]，于是
[*]
即g(x)在定义域上有界．
(3)[*]，从而h(x)在定义域Dh=(-∞，+∞)上无界．
(4)Dψ(-∞，+∞)，ψ(x+2k)=ψ[(x+k)+k]=[*]，即ψ(x)是定义域上以2k＞0为周期的连续周期函数，从而有界．
即四函数中在定义域有界的是f(x)，g(x)，ψ(x)；无界的是h(x)．
解析：[考点] 讨论函数在定义域内有界性
阅读以下关于嵌入式实时操作系统软件的选型分析方面的叙述，回答问题。
[说明]
某研究所承担了一项宇航嵌入式系统的研制任务，本项任务技术难度大，可靠性要求高，进度要求紧，预计软件规模约在一万行以上。而该所原先承担的相关项目均是用汇编语言编写的(软件规模较小，一般是几百行)。项目主管工程师将软件开发的论证工作分别布置给了架构师阮工和刘工，要求他们根据本项目的技术要求，在一周内分别提出软件的实施方案。
(1)该宇航嵌入式系统由数据处理机、信号处理机及数据采集模块组成。信号处理机主要通过数据采集模块将大量不固定时间周期的外部数据采集进来，进行预处理(如FFT变换)后提交给数据处理机；数据处理机根据功能要求完成各种计算处理工作，并将结果输出。为了达到数据处理机和信号处理机的标准化，这两类处理机均采用同种处理机的体系结构(如PowerPC 7410)。整个系统工作的最大周期为1s，最小周期为5ms。数据处理机上的任务分布如表3-10所示。
| 表3-10数据处理机上的任务分布表 | ||
| 工作周期 | 任务数(个) | 共占时间(ms) |
| 5 | 1 | 1 |
| 10 | 2 | 4 |
| 40 | 2 | 8 |
| 50 | 3 | 9 |
| 1000 | 2 | 3 |
[问题2]
选择实时嵌入式操作系统及开发环境时应考虑哪几方面问题请用200字以内的文字简要论证。