问题
问答题
当涉及的广义积分收敛时,试证以下积分等式:
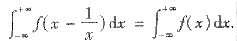
答案
参考答案:令[*],则当x→+∞时,t→+∞;当x→0+时,t→-∞;当x→0-时,t→+∞;当x→-∞时,t→-∞,故应以0为分界点,将[*]分解成两部分.
即[*]
同时将x与t的关系反解出来,得[*],于是
当x>0时,[*]
当x<0时,[*]
因此[*]
解析:[考点] 证明涉及广义积分的积分等式
当涉及的广义积分收敛时,试证以下积分等式:
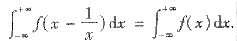
参考答案:令[*],则当x→+∞时,t→+∞;当x→0+时,t→-∞;当x→0-时,t→+∞;当x→-∞时,t→-∞,故应以0为分界点,将[*]分解成两部分.
即[*]
同时将x与t的关系反解出来,得[*],于是
当x>0时,[*]
当x<0时,[*]
因此[*]
解析:[考点] 证明涉及广义积分的积分等式