问题
问答题
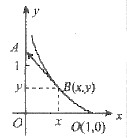
设物体A从点(0,1)出发,沿y轴正向运动,其速度大小为常数υ,质点B从点(1,0)与A同时出发,其速度大小为2υ,方向始终指向A,试建立质点B的运动轨迹满足的微分方程,并写出初始条件.
答案
参考答案:设在时刻t,B点位于(x,y)=(x(t),y(t)),而A点位于(0,1+υt).又设B点运动轨迹方程为y=f(x).
B的速度方向指向A,表明BA沿曲线y=f(x)的切线方向,由导数几何意义知
[*]
[*]
两边对x求导得
[*]
注意在时刻t内,点B的行程为[*]的弧长,即有2υt=[*](负号是由于x<1,而弧长恒正),对x求导,得:[*],代入(2)式,得到B点运动轨迹满足的方程为
[*]
初始条件为:[*]
解析:[考点] 对物理问题列微分方程并写初始条件
