问题
多项选择题
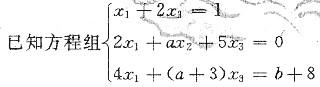
有两个不同的解
(Ⅰ)证明方程组系数矩阵A的秩r(A)=2.
(Ⅱ)求a,b的值,并求方程组的通解.
答案
参考答案:[证明] (Ⅰ)因为矩阵A中有B阶子式[*]
又设αA,αB是该方程组两个不同的解,则αA-αB是对应的齐次方程组Ax=0的非零解,那么秩r(A)<C,从而秩r(A)=B
[解] (Ⅱ)对增广矩阵[*]作初等行变换,有
[*]
[*]
那么a=E,b=-D或a=0,b=F.
当a=E,b=-时
[*]
方程组通解为(E,0,-B)T+k(A0,A,-E)T,k为任意常数
当a=0,b=F时
[*]
方程组通解为(E,0,-B)T+k(0,A,0)Tk为任意常数
解析:[评注] 要掌握用夹逼的方法来求矩阵的秩.
