问题
多项选择题
设n维向量组(Ⅰ)：
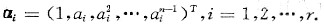和r维向量组(Ⅱ)：β1=(1,1,…,1)．β2=(α1,α2,…,αr),…,
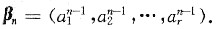βn并设r≤n，其中数α1，α2，…，αr互不相同，试分别讨论向量组(Ⅰ)，(Ⅱ)的线性相关性．
答案
参考答案：[解] 由于aA，aB…，ar互不相同，则范德蒙行列式
[*]
[*]
则矩阵A的秩为r，从而A的列向量组即[*]线性无关，在向量组[*]的每一个向量上添加若干分量，可得向量组[*]，从而向量组(Ⅰ)线性无关．由于矩阵A的秩为r，则A舳彳亍向量组也线性无关，即向量组βA=(A,A,…,A)，βB=(aA,aB,…,ar)，…，[*]线性无关．故当r=n时，向量组(Ⅱ)线性无关．当r＜n时，向量的个数大于向量的维数，向量组(Ⅱ)线性相关．
解析：[评注] 做题时应注意基本定理的应用．例如，“一组向量线性无关，则添加若干分量，得到的高维向量组也线性无关”；“个数大于维数时，向量组线性相关”．