问题
问答题
设A=(α1，α2，α3)是三阶矩阵，其中α1≠0，矩阵
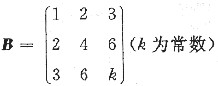且满足AB=0，求向量组α1，α2，α3的一个极大线性无关组，并将其余向量用这个极大线性无关组线性表示．
答案
参考答案：[解] 由AB=0故r(A)+r(B)≤3，又因A，B均非零矩阵，可知r(A)≥1，r(B)≥1．
当k≠9时秩r(B)=2，于是秩r(A)=1；
当k=9时秩r(B)=1，于是秩r(A)=1或r(A)=2．
(1)当k≠9时，向量组α1，α2，α3的极大线性无关组是α1．
由AB=0，有
[*]
得
(9-k)α3=0
所以
α3=0，α1+2α2=0．
因此
[*]
(2)当k=9时，
如果r(A)=1，则α1，α2，α3的极大线性无关组是α1．
由 α1+2α2+3α3=0
[*]
如果r(A)=2，则α1，α2，α3必两两线性无关，极大线性无关组是α1，α2．
而
[*]
解析：[评注] 对于AB=0要有两个基本构思：
(1)r(A)+r(B)≤n (2)B的列向量是齐次方程组Ax=0的解．