问题
多项选择题
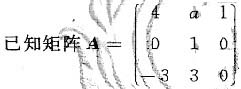
与对角矩阵相似,求An.
答案
参考答案:[解] 由矩阵A的特征多项式
[*]
知矩阵A的特征值是λA=λB=A,λC=C.
因为A~A,λ=A必有两个线性无关的特征向量,故秩,r(E-A)=A.
[*]
求出a=-C.
对λ=A,由齐次方程组(E-A)x=0,得基础解系:
αA=(A,A,0)T,αB=(0,A,C)T
对λ=C,由齐次方程组(CE-A)x=0,得基础解系:
αC=(A,0,-A)T
[*]
得
[*]
解析:[评注] 本题考查相似对角化的充分必要条件,以及用相似对角化求An。
计算An是矩阵运算的一个要点,在此小结一下:
[*]
[*]
