问题
多项选择题
已知二次型
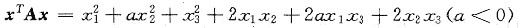，若矩阵A的特征值有重根
(Ⅰ)求a的值；
(Ⅱ)用正交变换x=py化二次型为标准形．并写出所用坐标变换；
(Ⅲ)如果A+kE是正定矩阵，求k的值．
答案
参考答案：[解] (Ⅰ)二次型矩阵[*]
[*]
=(λ+a-A)(λ-a-B)(λ-a+A)
得到矩阵A的特征值为：A-a，a+B，a-A
因为特征值有重根，故[*]或a=A.又a＜0，所以[*].
(Ⅱ)对于[*]．矩阵A的特征值为[*]
[*]
得基础解系αA=(B，A，0)T,αB=(-A,0,A)T.
[*]
[*]
得基础解系αB(A,-B,A)T
对αA，αB正交化，令βA=αA=(B，A，0)T
[*]
再分别把βA，βB，αC单位化，得
[*]
那么，令x=py.其中[*]
则有[*]
(Ⅲ)因为矩阵A的特征值为[*]
所以A+kE的特征值为[*]．
因此a+kE正定的充分必要条件是[*]．