问题
多项选择题
(Ⅰ)设A是m×n矩阵,β是任一个m维列向量,证明方程组Ax=β有解的充分必要条件是秩r(A)=m.
(Ⅱ)
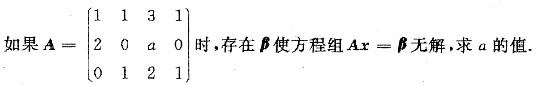
答案
参考答案:[证明] (Ⅰ)必要性 设A=(αA,αB,…,αn)其中αA,αB,…,αn是m维列向量.
对任意的m维列向量β,方程组Ax=β有解,等价于αA,αB,…,αn可以表示任意一个m维列向量.那么αA,αB,…,αn可以线性表示m维单位向量eA=(A,0,…,0)T,eB=(0,A,…,0)T,…,em=(0,0,…,A)T.
于是秩r(eA,eB,…,em)≤r(αA,αB,…,αn)=r(A)
又秩r(eA,eB,…,em)=m.
且
r(A)≤m.
所以
r(A)=m.
充分性 A是m×n矩阵,[*]=(A,β)是m×(n+A)矩阵,因为r(A)=m.即A中有m阶子式不为0.那么[*]必有m阶子式不为0,所以必有r([*])=m.于是r(A)=r([*])方程组Ax=β必有解.
[解] (Ⅱ) 由(Ⅰ)知若存在β使方程组Ax=β无解,则秩r(A)<C.对A作初等变换,有
[*]
故
a=B
