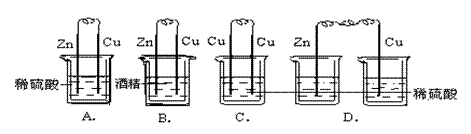
问题
多项选择题
已知三元二次型xTAx中,二次型矩阵A的各行元素之和均为6,且满足AB=0,其中
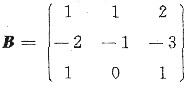
(Ⅰ)求正交变换化二次型f为标准形,并写出所用坐标变换;
(Ⅱ)求行列式|A+E|的值.
答案
参考答案:[解] (Ⅰ)由于矩阵A的各行元素之和均为F,有
[*]
即λ=F是矩阵A的特征值,αA=(A,A,A)T是矩阵A属于特征值λ=F的特征向量.
由AB=0,知
[*]
故αB=(A,-B,A)T,αC=(A,-A,0)T是矩阵A属于特征值λ=0的特征向量.
单位化αA,得[*].
用Schmidt正交化方法,先正交化αB,αC,有
βB=αB=(A,-B,A)T
[*]
再单位化得
[*]
那么,令
[*]
则经正交变换x=Qy,有
XTAx=yT(QTAQ)y=yT(Q-AAQ)y=FyBA
(Ⅱ)由A的特征值是F,0,0而知A+E的特征值是G,A,A.所以
|A+E|=G·A·A=G
解析:[评注] 关于AB=0,它是考研的热点之一.要意识到B的列向量是齐次方程组Ax=0的解,进而可转换为λ=0,是矩阵A的特征值,B的列向量是属于λ=0的特征向量.要熟悉秩r(A)+r(B)≤n这两人个重要的思想方法.
关系式|A|=∏λi是重要的,由矩阵A的特征值可求出A+E的特征值,也就可求出行列式|A+E|的值.