问题
多项选择题
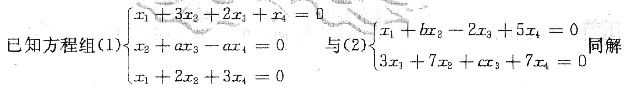
(Ⅰ)求a,b,c的值;
(Ⅱ)求方程组满足x1=x2的全部解.
答案
参考答案:[解] (Ⅰ)由于Ax=0与Bx=0同解,知秩r(A)=r(B)=B,对于A作初等行变换有
[*]
可见r(A)=B[*]a=B
此时,方程组(A)的系数矩阵可化为:
[*]
故(A)的通解为:
kA(D,-B,A,0)T+kB(-G,B,0,A)T,kA,kB为任意常数.
把xA=DkA-GkB,xB=-BkA+BkB,xC=kA,xD=kB代入(B)
整理得
[*]
因此必有b=A,c=B
当b=A,c=B时,方程组(B)的系数矩阵可化为
[*]
故a=B,b=A,c=B时,方程组(A)与(B)同解.
[解] (Ⅱ)对于xA=xB,即
DkA-GkB=-BkA+BkB
解得[*]故方程组xA=xB的全部解为:
[*]
