参考答案：

由题设条件知，r(C)+r(B)=n已知(A+E)C=O，B(A^T-2E)=O，若r(C)=n，则r(B)=0，由(A+E)C=O，两边右乘C^-1得A+E=0，

即A=-E． 故A～Λ=-E．

若r(B)n，则r(C)=0，由B(A_T-2E)=O，两边左乘B^-1，得A^T-2E=O，

即A^T=2E． 故A=(2E)^T=2E～Λ=2E．

若r(C)=r，r≠n，r≠0，则r(B)=n-r．

由(A+E)C=O，将C以列分块，方程组(A+E)X=0至少有r个线性无关解向量．

即A有特征值λ=-1，且至少是r重根．

由B(A^T-2E)=O，两边转置得

(A-(2E)^T)B^T=(A-2E)B^T，

因r(B^T)=r(B)=n-r，故将B^T以列分块，知方程组(A-2E)X=0至少有n-r个线性无关解．即A有特征值λ=2，且至少有n-r重根．

因r(B)+r(C)=n．故λ=-1是r重根，λ=2是n-r重根，

且A有n个线性无关特征向量，故A～Λ，其中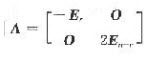

且|A|=|Λ|=(-1)^r2^n-r．