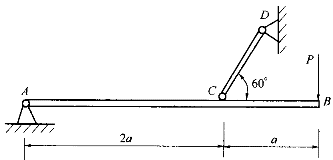
问题
解答题
设椭圆的中心是坐标原点,长轴在x轴上,离心率e=
|
答案
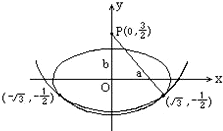
根据题设条件,可取椭圆的参数方程是
,其中0≤θ<2π,x=acosθ y=bsinθ
由e2=
=1-(c2 a2
)2可得b a
=b a
=1-e2
=1- 3 4
,即a=2b.1 2
设椭圆上的点(x,y)到点P的距离为d,则
d2=x2+(y-
)23 2
=a2cos2θ+(bsinθ-
)23 2
=a2-(a2-b2) sin2θ-3bsinθ+9 4
=4b2-3b2sin2θ-3bsinθ+9 4
=-3b2(sinθ+
)2+4b2+3.1 2b
如果
>1,即b<1 2b
,则当sinθ=-1时,d2有最大值,由题设得(1 2
)2=(b+7
)2,3 2
由此得b=
-7
>3 2
,与b<1 2
矛盾.1 2
因此必有
≤1成立,于是当sinθ=-1 2b
时,d2有最大值,由题设得(1 2b
)2=4b2+3,7
由此可得b=1,a=2.
所求椭圆的参数方程是
,由sinθ=-x=2cosθ y=sinθ
,cosθ=±1 2
可得,3 2
椭圆上的点(-
,-3
)和(1 2
,-3
)到点P的距离都是1 2
.7