椭圆

x2

16

+

y2

4

=1的左右焦点分别为F₁（-2

3

，0）、与F₂（2

3

，0）．

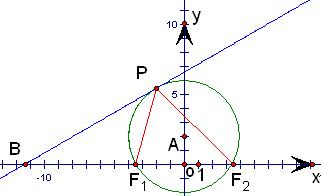
如图，根据平面几何知识知，当∠F₁PF₂取最大值时，经过F₁与F₂，的圆与直线l 相切，此时圆心在y轴上，坐标为A（0，2），

在直线l：x-

3

y+8+2

3

=0中令y=0得B的坐标：

B（-8-2

3

，0），

在三角形BPF₁和三角形BF₂P中，∠BPF₁=∠BF₂P，

∴△BPF₁∽△BF₂P，

∴

|PF 1|

|PF 2|

=

PB

BF 2

=

AB 2-PA 2

BO+OF 2

=

3

-1．

故答案为：

3

-1．