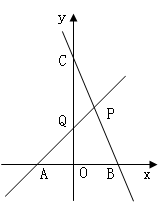
如图，在平面直角坐标系xOy中，已知直线PA是一次函数y=x＋m（m＞0）的图象，直线PB是一次函数y=－3x＋n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点．
（1）用m、n分别表示点A、B、P的坐标及∠PAB的度数；
（2）若四边形PQOB的面积是4，且CQ：AO=2：1，试求点P的坐标，并求出直线PA与PB的函数表达式；
（3）在（2）的条件下，是否存在一点D，使以A、B、P、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由．
（1）A（-m，0），B（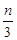
，0）．P（
，
），∠PAB=45°
（2）PA的函数表达式为y=x+2，PB的函数表达式为y=-3x+6．
（3）存在．D1(5，3)、D2(−3,3)、D3(−1，-3)．
题目分析：（1）在直线y=x+m中，令y=0，得x=-m．
∴点A（-m，0）．
在直线y=-3x+n中，令y=0，得x＝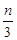
∴点B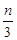（，0）．
由
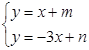，得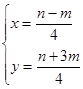
，
∴点P（，）
在直线y=x+m中，令x=0，得y=m，
∴|-m|=|m|，即有AO=QO．
又∠AOQ=90°，
∴△AOQ是等腰直角三角形，
∴∠PAB=45°．
（2）∵CQ：AO=2：1，
∴（n-m）：m=2：1，
整理得n =3m，
∴=
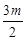
而S四边形PQOB=S△PAB-S△AOQ=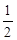
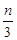（+m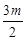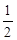）·-m2=m2=4，
解得m=±2，
∵m＞0，
∴m=2，
∴n="3m" =6，
∴P（1，3）．
∴PA的函数表达式为y=x+2，
PB的函数表达式为y=-3x+6．
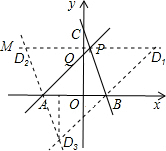
（3）存在．
过点P作直线PM平行于x轴，过点B作AP的平行线交PM于点D1，过点A作BP的平行线交PM于点D2，过点A、B分别作BP、AP的平行线交于点D3．
①∵PD1∥AB且BD1∥AP，
∴PABD1是平行四边形．此时PD1=AB，易得D1(5，3)；
②∵PD2∥AB且AD2∥BP，
∴PBAD2是平行四边形．此时PD2=AB，易得D2(−3,3)；
③∵BD3∥AP且AD3∥BP，此时BPAD3是平行四边形．
∵BD3∥AP且B（2，O），∴D3(−1，-3)．