ABC公司的一种新型产品原有信用政策n/30,每天平均销量为20个,每个售价为 75元,平均收账天数40天;公司销售人员提出了新的政策,以便促销产品,新的政策包括改变信用政策:“2/10,n/50”,同时以每个60元的价格销售,预计改变政策后每天能多售出60个,估计80%的客户会享受折扣,预计平均收账天数为45天,新政策同时需要增加8万元的广告费。企业资本成本率为10%,存货单位变动年储存成本是9元,每次订货成本为225元,该新型产品的每个购买价格为50元。
要求:
(1) 计算公司该产品改变政策前后的经济订货量和最佳订货次数;
(2) 若单位缺货成本为5元,存货正常交货期为10天,延迟交货1天的概率为0.2,延迟交货2天的概率为0.1,不延迟交货的概率为0.7,计算合理的保险储备和再订货点;
(3) 按照第(1)和第(2)问所确定的经济订货量和再订货点进行采购,综合判断应否改变政策。
参考答案:
(1) 原政策:
年销量=20×360=7200(个)
经济订货量
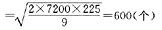
订货次数=7200/600=12(次)
新政策;
年销量=80×360=28800(个)
经济订货量
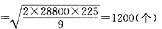
订货次数=28800/1200=24(次)
(2)改变政策前:
每天需要量20个,正常交货期内需要量=10×20=200(个)
若延期交货1天,则交货期内的需要量=11×20=220(个)
若延期交货2天,则交货期内的需要量=12×20=240(个)
不设保险储备(即B=0)时:
再订货点=200+0=200(个)
缺货量S=(220-200)×0.2+(240-200)×0.1=8(个)
相关成本TC(S,B)=5×8×12=480(元)
保险储备为20个(即B=20)时:
再订货点=200+20=220(个)
缺货量S=(240-220)×0.1=2(个)
相关成本TC(S,B)=5×2×12+20×9=300(元)
保险储备为40个(即B=40)时:
再订货点=200+40=240(个)
缺货量S=0
相关成本TC(S,B)=40×9=360(元)
所以合理保险储备为20个,再订货点为220个。
改变政策后:
每天需要量80个,正常交货期内需要量=10×80=800(个)
若延期交货1天,则交货期内的需要量=11×80=880(个)
若延期交货2天,则交货期内的需要量=12×80=960(个)
不设保险储备(即B=0)时:
再订货点=800+0=800(个)
缺货量S=(880-800)×0.2+(960-800)×0.1=32(个)
相关成本TC(S,B)=5×32×24=3840(元)
保险储备为80个(即B=80)时:
再订货点=800+80=880(个)
缺货量S=(960-880)×0.1=8(个)
相关成本TC(S,B)=5×8×24+80×9=1680(元)
保险储备为160个(即B=160)时:
再订货点=800+160=960(个)
缺货量S=0
相关成本TC(S,B)=160×9=1440(元)
所以合理保险储备为160个,再订货点为960个。
(3) 税前收益增加额
单位:元

结论:不应该改变政策。
