问题
选择题
一动圆与圆O:x2+y2=1外切,与圆C:x2+y2-6x+8=0内切,那么动圆的圆心的轨迹是( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
答案
答案:C
题目分析:由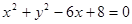 ,可得
,可得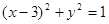 ,设动圆圆心为
,设动圆圆心为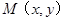 ,半径为
,半径为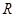 ,∵圆
,∵圆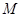 与圆
与圆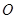 外切,∴
外切,∴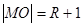 ,∵圆
,∵圆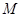 与圆
与圆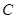 内切,∴
内切,∴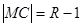 ,从而
,从而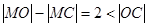 ,根据双曲线的定义,动圆圆心的轨迹是是以
,根据双曲线的定义,动圆圆心的轨迹是是以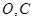 为焦点的双曲线(靠近点
为焦点的双曲线(靠近点 的一支).
的一支).
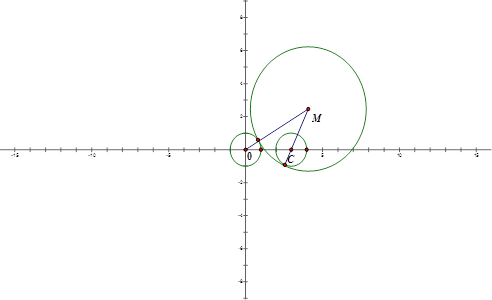
一动圆与圆O:x2+y2=1外切,与圆C:x2+y2-6x+8=0内切,那么动圆的圆心的轨迹是( )
A.圆
B.椭圆
C.双曲线的一支
D.抛物线
答案:C
题目分析:由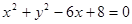 ,可得
,可得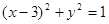 ,设动圆圆心为
,设动圆圆心为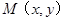 ,半径为
,半径为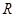 ,∵圆
,∵圆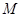 与圆
与圆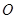 外切,∴
外切,∴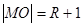 ,∵圆
,∵圆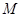 与圆
与圆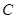 内切,∴
内切,∴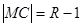 ,从而
,从而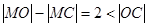 ,根据双曲线的定义,动圆圆心的轨迹是是以
,根据双曲线的定义,动圆圆心的轨迹是是以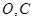 为焦点的双曲线(靠近点
为焦点的双曲线(靠近点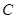 的一支).
的一支).
