问题
问答题
设A为m×n矩阵,且

1.证明方程组AX=b有且仅有n-r+1个线性无关解;
答案
参考答案:
 =β.因为AX=β有三个非零解,所以AX=0有两个非零解,故4-r(A)≥2,r(A)≤2,又因为r(A)≥2,所以r(A)=r(
=β.因为AX=β有三个非零解,所以AX=0有两个非零解,故4-r(A)≥2,r(A)≤2,又因为r(A)≥2,所以r(A)=r(
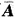 )=2.
)=2.

设A为m×n矩阵,且

1.证明方程组AX=b有且仅有n-r+1个线性无关解;
参考答案:
 =β.因为AX=β有三个非零解,所以AX=0有两个非零解,故4-r(A)≥2,r(A)≤2,又因为r(A)≥2,所以r(A)=r(
=β.因为AX=β有三个非零解,所以AX=0有两个非零解,故4-r(A)≥2,r(A)≤2,又因为r(A)≥2,所以r(A)=r(
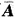 )=2.
)=2.
