问题
解答题
一束光线从点F1(﹣1,0)出发,经直线l:2x﹣y+3=0上一点P反射后,恰好穿过点F2(1,0).
(Ⅰ)求点F1关于直线l的对称点F1'的坐标;
(Ⅱ)求以F1、F2为焦点且过点P的椭圆C的方程;
(Ⅲ)设直线l与椭圆C的两条准线分别交于A、B两点,点Q为线段AB上的动点,求点Q 到F2的距离与到椭圆C右准线的距离之比的最小值,并求取得最小值时点Q的坐标.
答案
解:(Ⅰ)设F1的坐标为(m,n),则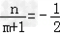 且
且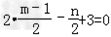 .
.
解得 ,因此,点F1'的坐标为(﹣
,因此,点F1'的坐标为(﹣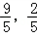 ).
).
(Ⅱ)∵|PF1'|=|PF1|,根据椭圆定义,
得2a=|PF1'|+|PF2|=|F1F2|=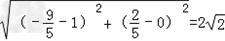 ,
,
∴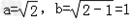 .
.
∴所求椭圆方程为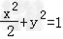 .
.
(Ⅲ)∵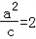 ,∴椭圆的准线方程为x=±2.
,∴椭圆的准线方程为x=±2.
设点Q的坐标为(t,2t+3)(﹣2<t<2),d1表示点Q到F2的距离,d2表示点Q到椭圆的右准线的距离.
则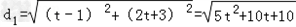 ,
,
d2=|t﹣2|.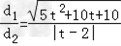 =
=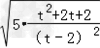 ,
,
令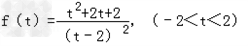 ,则
,则
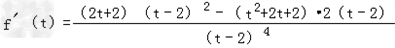 =
=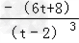 ,
,
∵当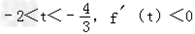 ,
, ,t=﹣
,t=﹣ ,f'(t)>0.
,f'(t)>0.
∴f(t)在t=﹣ 时取得最小值.
时取得最小值.
因此, 最小值=
最小值= ,此时点Q的坐标为(﹣
,此时点Q的坐标为(﹣ )
)
